DEC-10 Lab

AI Terms

Posted on Edited on In Valine: 7.7k 7 mins.

Bootstrapping

  1. In general
  • a self-starting process that is supposed to proceed without external input.
  1. In computer technology(usually shortened to booting)
  • the process of loading the basic software into the memory of a computer after power-on or general reset, especially the operating system which will then take care of loading other softwares as needed.
  • Booting is the process of starting a computer, specifically with regard to starting its software.
  1. Origins
  • in the early 19th-century United States (particularly in the phrase “pull oneself over a fence by one’s bootstraps”).
  1. A more practical and common interpretation
  • the phrase infers that when a person wants to succeed, the first thing they need to do before hard work, is to put on their boots. In this sense, the phrase makes perfect sense, as most working Americans put their shoes or boots on as the last item of clothing before they start for work.
  1. In Artificial Intelligence(AI) and Machine Learning(ML)
  • a technique used to iteratively improve a classifier’s performance.
  • Typically, multiple classifiers will be trained on different sets of the input data, and on prediction tasks the output of the different classifiers will be combined together.
  1. In statistics
  • the practice of estimating properties of an estimator (such as its variance) by measuring those properties when sampling from an approximating distribution.

自助（抽样）法

基本概念

  • 自身样本重采样的方法来估计真实分布的问题

  • 从给定训练集中有放回的均匀抽样（每当选中一个样本，它等可能地被再次选中并被再次添加到训练集中。）

  • 对于小数据集，自助法效果很好。

  • 最常用的一种是.632自助法，假设给定的数据集包含d个样本。该数据集有放回地抽样d次，产生d个样本的训练集。这样原数据样本中的某些样本很可能在该样本集中出现多次。没有进入该训练集的样本最终形成检验集（测试集）。 显然每个样本被选中的概率是1/d，因此未被选中的概率就是(1-1/d)，这样一个样本在训练集中没出现的概率就是d次都未被选中的概率，即(1-1/d)^d。当d趋于无穷大时，这一概率就将趋近于e^(-1)=0.368，所以留在训练集中的样本大概就占原来数据集的63.2%。

  • 对于这部分大约36.8%的没有被采样到的数据，我们常常称之为袋外数据(Out Of Bag, 简称OOB)。这些数据没有参与训练集模型的拟合，因此可以用来检测模型的泛化能力。

  • 为了从单个样本中产生多个样本，bootstrapping作为交叉验证的一个替代方法，在原来的样本中进行替换的随机采样，从而得到新的样本。bootstrap得到的样本比交叉验证的样本重叠更多，因此它们的估计依赖性更强，被认为是小数据集进行重采样的最好方法。

  • 例子：我要统计鱼塘里面的鱼的条数，怎么统计呢？假设鱼塘总共有鱼1000条，我是开了上帝视角的，但是你是不知道里面有多少。
    步骤：

    1. 承包鱼塘，不让别人捞鱼(规定总体分布不变)。
    2. 自己捞鱼，捞100条，都打上标签(构造样本)
    3. 把鱼放回鱼塘，休息一晚(使之混入整个鱼群，确保之后抽样随机)
    4. 开始捞鱼，每次捞100条，数一下，自己昨天标记的鱼有多少条，占比多少(一次重采样取分布)。
    5. 重复3，4步骤n次。建立分布。
      假设一下，第一次重新捕鱼100条，发现里面有标记的鱼12条，记下为12%，放回去，再捕鱼100条，发现标记的为9条，记下9%，重复重复好多次之后，假设取置信区间95%，你会发现，每次捕鱼平均在10条左右有标记，所以，我们可以大致推测出鱼塘有1000条左右。其实是一个很简单的类似于一个比例问题。这也是因为提出者Efron给统计学顶级期刊投稿的时候被拒绝的理由–”太简单”。这也就解释了，为什么在小样本的时候，bootstrap效果较好，你这样想，如果我想统计大海里有多少鱼，你标记100000条也没用啊，因为实际数量太过庞大，你取的样本相比于太过渺小，最实际的就是，你下次再捕100000的时候，发现一条都没有标记，，，这特么就尴尬了。。。

  • 其核心思想和基本步骤如下：

    • 采用重抽样技术从原始样本中抽取一定数量（自己给定）的样本，此过程允许重复抽样。
    • 根据抽出的样本计算给定的统计量T。
    • 重复上述N次（一般大于1000），得到N个统计量T。
    • 计算上述N个统计量T的样本方差，得到统计量的方差。

  • 通过方差的估计可以构造置信区间等

  • 整合多个弱分类器，成为一个强大的分类器。这时候，集合分类器(Boosting, Bagging等)出现了。

集成学习（ensemble learning）

  • 将若干弱分类器组合之后产生一个强分类器
  • 弱分类器（weak learner）指那些分类准确率只稍好于随机猜测的分类器（error rate < 50%）
  • 假设各弱分类器间具有一定差异性（如不同的算法，或相同算法不同参数配置），这会导致生成的分类决策边界不同，也就是说它们在决策时会犯不同的错误。将它们结合后能得到更合理的边界，减少整体错误，实现更好的分类效果。
  • 数据集较大时，可以分为不同的子集，分别进行训练，然后再合成分类器。
    数据集过小时，可使用自助法（bootstrapping），从原样本集有放回的抽取m个子集，训练m个分类器，进行集成。
  • bagging和boosting都是集成学习（ensemble learning）领域的基本算法

Bagging(bootstrap aggregation)

  • 从训练集从进行子抽样组成每个基模型所需要的子训练集，对所有基模型预测的结果进行综合产生最终的预测结果,至于为什么叫bootstrap aggregation，因为它抽取训练样本的时候采用的就是bootstrap的方法！

  • 让该学习算法训练多轮，每轮的训练集由从初始的训练集中随机取出n个训练样本组成，某个训练样本在某训练集中可能出现多次或者不出现，训练之后可得到一个预测函数序列h_1,h_n，最终的预测函数H对分类问题采用投票方式，对回归问题（加权平均好点，但是没）采用简单平均方式判别。训练R个分类器f_i,分类器之间其他相同就是参数步相同。其中f_i是通过从训练集和中随机取N次样本训练得到的。对于新样本，用这个R个分类器去分类，得到最多的那个类别就是这个样本的最终类别。

Bagging代表算法-Random Forest(随机森林)

  • Bootstrap方法随机选择子样本

  • 属性集中随机选择k个属性，每个树节点分裂时，从这随机的k个属性，选择最优的

  • 随机森林，使用随机的方式建立一个森林，森林里面有很多的决策树组成，随机森林的每一棵决策树之间是没有关联的。在得到森林之后，当有一个新的输入样本进入，就让森林中的每一棵决策树分别进行判断，看看这个样本属于那个类，然后看看哪一类被选择多，就预测为那一类。

  • 在建立决策树的过程中，需要注意两点-采样和完全分裂。首先是两个随机采样的过程，Random Forest对输入的数据要进行 行，列的采样。

  • 对于行采样，采用有放回的方式，也就是在采样得到的样本集合中，可能有重复的样本。假设输入样本为N个，那么采样的样本也为n个。这样使得在训练的时候，每一棵树的输入样本都不是全部样本，使得相对不容易出现over-fitting。

  • 然后进行列采样，从M个feature中，选择m个。

  • 之后就是对采样之后的数据使用完全分裂的方式建立出决策树，这样决策树的某一个叶子节点要么是无法继续分裂，要么里面的所有样本都是指向的同一类分类。

  • 一般的决策树都有一个重要的步骤，剪枝，但是这里不这样干，由于之前的两个随机采样的过程保证了随机性，所以就算不剪枝，也不会over-fitting。

  • 按这种算法得到的随机森林中的每一棵树都是很弱的，但是组合起来就很厉害了。可以这样比喻随机森林：每一颗决策树就是一个精通于某一个窄领域的专家，这样在随机森林中就有了很多个精通不同领域的专家，对于新的样本，可以用不同的角度看待它，最终由各个专家，投票得到结果。

Boosting算法代表–Adaboost(Adaptive Boosting)

  • 初始化时对每一个训练赋予相同的权重1/n（每个样本都是等概率的分布，每个分类器都会公正对待），然后用该算法对训练集训练t轮，每次训练后，对训练失败的训练列赋予较大的权重（通常是边界附近的样本），也就是让学习算法在后续的学习中集中对比较难的训练列进行训练（就是把训练分类错了的样本，再次拿出来训练，看它以后还敢出错不），整个迭代过程直到错误率足够小或达到一定次数为止，从而得到一个预测函数序列h_1,h_m，其中h_i也有一定的权重，预测效果好的预测函数权重大，反之小。最终的预测函数H对分类问题采用有权重的投票方式，对回归问题采用加权平均的方式对新样本判别。

  • 类似bagging方法，但是训练是串行的（顺序生成），第K个分类器训练时，关注对前k-1分类器中错误，不是随机取样本，而是加大取这些分错的样本的权重。

区别

  • 取样本方式不同：bagging采用均匀取样，而boosting根据错误率来采样，因此boosting的分类精度要由于bagging。
  • bagging的训练集选择是随机的，各轮训练集之前互相独立，而boosting的各轮训练集的选择与前面各轮的学习结果相关；bagging的各个预测函数没有权重，而boosting有权重；
  • bagging的各个函数可以并行生成，而boosting的各个预测函数只能顺序生成。
  • 对于像神经网络这样极为消耗时间的算法，bagging可通过并行节省大量的时间开销。bagging和boosting都可以有效地提高分类的准确性。在大多数数据集中，boosting的准确性要比bagging高。有一些数据集中，boosting会退化-overfit。boosting思想的一种改进型adaboost方法在邮件过滤，文本分类中有很好的性能。

置信区间，就是一种区间估计。

  • 例子：
    • 人口平均身高统计，这个数据肯定存在的，但只有上帝知道
    • 人类统计的方法是抽样统计（不可能每个人的身高都统计到）
    • 如果采用点估计，使用抽样的数据可以得到一个样本均值（平均身高），这样通过不同的抽样，就会得到不同的样本均值
    • 问题来了，这样不知道哪个点估计更好
    • 而采用区间估计的区间都包含了真实的期望值（真实的平均身高）
    • 问题又来了，这样不知道哪个区间估计更好
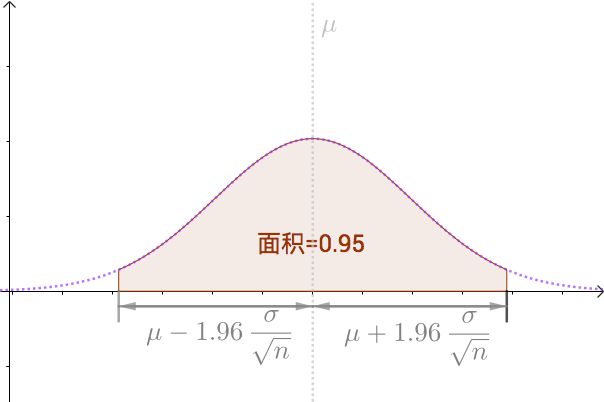
    • 95% 的置信区间，就是有95%的概率使估计的区间内包含期望值（构造100个这样的区间，大约会有95个区间包含期望值）
    • The 95% confidence interval defines a range of values that you can be 95% certain contains the population mean. With large samples, you know that mean with much more precision than you do with a small sample, so the confidence interval is quite narrow when computed from a large sample.
      confidence interval

Bootstrapping programming in R

If we have n data entries, indexed as y1,…,yn and x1,…,xn, we can generate a new data set by sampling from these indices uniformly with replacement. Lets see how to do this in R using the faithful data set:

1
2
3
data = faithful
bootstrap_indices = sample(length(faithful), length(faithful), replace=TRUE)
data_bootstrap = data[bootstrap_indices, ]

data_bootstrap is now a bootstrap sample from the original data.

There is little to be gained from BAGGING linear regressions. This is because the sum of two linear functions is another linear function. However, for non-linear functions there is much more potential. For example,the sum of many logistic functions is not in general another logistic function. Therefore we will use logistic regression to demonstrate the power of BAGGING. We’ll define an underlying probability function that is impossible for a single logistic regression to capture properly. Then we'll show how summing over many logistic regression models trained on different sampled subsets of the data can outperform a single model.

1
2
3
4
5
6
7
8
9
#define a complex probability function
myfunction <- function(x){0+1*(x>0.25 & x < 0.75)}
#Generate some data
X = seq(0,1, length.out=100)
P = myfunction(X)
Y = as.numeric(runif(100)<P)
#Plot the data with the actual probability
plot(X, Y)
lines(X, P)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
#Make a data frame and split into training and test data
mydata = data.frame(Y, X)
test_idx = sample(dim(mydata)[1], 20)
test_data = mydata[test_idx, ]
train_data = mydata[-test_idx, ]
#Fit a logistic model to the training data
myModel = glm(Y ~ X, data=train_data, family=binomial)
#Make a prediction for the probability of the test data being 1
prediction = predict(myModel, newdata=test_data, type="response")
#Evaluate the predictive log-likelihood
testLL = sum(log(prediction[which(test_data$Y==1)])) +
  sum(log(1-prediction[which(test_data$Y==0)]))

#BAGGING!

#Make 1000 bootstrap samples
#Fit a logistic model to each
#Record prediction onto test data and aggregate
bsPrediction = rep(0, dim(test_data)[1])
for (i in 1:1000){
  bs_idx = sample(dim(train_data)[1], 20, replace=TRUE)
  bs_data = train_data[bs_idx,]
  bsModel = glm(Y ~ X, data=bs_data, family=binomial)
  bsPrediction = bsPrediction + predict(bsModel, newdata=test_data, type="response")/1000
}
#Get the predictive likelihood of the bagged model
bstestLL = sum(log(bsPrediction[which(test_data$Y==1)])) +
  sum(log(1-bsPrediction[which(test_data$Y==0)]))
1
2
#Print the results
print(testLL)
1
print(bstestLL)
1
2
plot(test_data$X, prediction)
plot(test_data$X, bsPrediction)

In this case a single logistic regression cannot capture the fact that the probability is non-monotonic in X. By learning from different sampled subsets of the data, the BAGGED logistic regressions capture different features of the underlying relationship, in this case the rise in probability at X = 0.25 and th decrease at X = 0.75.

Reference:

  1. tutorial from Professor Netta Cohen
  2. lectures from university of leeds
  3. wikipedia
  4. 简书
  5. 机器之心
  6. 知乎
Related Posts
Persist in original technology sharing, your support will encourage me to continue to create!